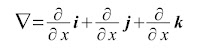Mappa delle offerte di lavoro GIS

The GIS Jobs Clearinghouse Map rappresenta in mappa offerte di lavoro GIS:
http://www.gjc.org/map.html.

E basandosi sulla mappa l'Europa non appare brillare...

GoogleMars

Istruzioni per visitare Marte.

Get Flash to see this player.

Operatori vettoriali nei GIS: il gradiente

Nei GIS i procedimenti e le visualizzazioni di dati vettoriali non sono molto diffuse, fatto salvo il caso del calcolo delle pendenze topografiche. I GIS calcolano implicitamente un campo vettoriale, tramite due distinti campi scalari, l'esposizione (aspect) e la pendenza (slope), che esprimono rispettivamente l'orientazione della massima inclinazione rispetto al nord della mappa ed il valore di inclinazione rispetto al piano orizzontale.

Questo campo vettoriale corrisponde al gradiente di un campo scalare, l'elevazione. Il gradiente viene calcolato applicando ad una superficie scalare ϕ(x,y,z), supposta continua e derivabile in ogni punto, l'operatore differenziale vettoriale nabla:

Nel caso di una superficie topografica la superficie è funzione di due soli variabili spaziali, x e y, per cui z = ϕ(x,y) e il suo gradiente vale:

Il risultato è un campo vettoriale bi-dimensionale su un piano orizzontale. Per ogni punto del dominio spaziale, il vettore orizzontale punta nella direzione di massima pendenza della topografia ed ha un modulo proporzionale alla pendenza di questa.

Con linguaggi di scripting e software open source è possibile calcolare e visualizzare questo campo vettoriale come entità singola, non scissa in esposizione e pendenza. In questo post vediamo un esempio che si basa su Python per il processamento e su ParaView per la visualizzazione.

Dato che nella realtà le superfici topografiche non sono rappresentate da superfici analitiche ma da misure discrete nello spazio, una implementazione del calcolo del gradiente si deve basare su dati discreti, archiviati in formati come il raster a celle quadrate. Esistono varie formulazioni per il calcolo del gradiente nei GIS. Quella di base, implementata per esempio in Surfer, calcola i due gradienti lungo le direzioni x e y come differenze discrete tra i valori delle due celle contigue alla cella centrale.

dz/dx = [ Elev(i, j + 1) - Elev(i, j - 1) ] / 2*cell_size

dz/dy = [ Elev(i - 1, j) - Elev(i + 1, j) ] / 2*cell_size

In questo script Python, modificato da quello precedentemente creato per il calcolo della pendenza lungo direzioni variabili nello spazio, questa formulazione fornisce la possibilità di definire la distanza delle due celle laterali o verticali dalla cella centrale, in maniera tale da utilizzarlo come un fattore di smoothing che regola la risoluzione effettiva per la quale il gradiente è calcolato.

dz/dx = [ Elev(i, j + n) - Elev(i, j - n) ] / 2*n*cell_size

dz/dy = [ Elev(i - n, j) - Elev(i + n, j) ] / 2*n*cell_size

Il valore rappresenta il numero di celle a sinistra e a destra per la differenza lungo le x, o sopra e sotto per le y, utilizzate nel calcolo (esempio con smoothing factor uguale a 2 in figura sottostante).

Lo script Python calcola le componenti lungo i due assi a partire da un file ascii nel formato ESRI grid e le salva, assieme ai valori di elevazione, in un file ascii nel formato vtk (legacy vtk format). Col software ParaView è possibile visualizzare ed elaborare questi dati scalari e vettoriali. ParaView non è particolarmente intuitivo come utilizzo, ma con alcuni tentativi si riesce a capire quali sono le funzioni di base utili per visualizzare dati.

Usiamo dati liberi dello Shuttle Radar Topography Mission (SRTM2), con risoluzione nominale di 90 m, del lago di Bolsena, nel Lazio.

Il modulo del campo vettoriale viene calcolato automaticamente da ParaView, a partire dalle sue componenti.

Queste stesse componenti sono visualizzabili e rendono bene l'andamento morfologico della superficie, meno evidente dalle immagini satellitari, e che consiste in caldere di varie dimensioni, fra loro coalescenti. I valori positivi delle componenti indicano salite spostandosi da ovest verso est, nel caso del gradiente lungo le x, e dall'alto verso il basso, per il gradiente lungo le y.

Ed infine, il campo vettoriale può essere rappresentato utilizzando una serie di glifi che indicano l'orientazione dei vettori ed il loro modulo, sempre a partire dalle singole componenti cartesiane. Ovviamente anche nei GIS è possibile rappresentare questa informazione, ma occorre calcolare il valore angolare dell'orientazione ed utilizzarlo come campo di rotazione del glifo. Nella figura sottostante è rappresentato il campo vettoriale per un settore limitato della zona considerata.

Lunedì 28 giugno: Live broadcast (gratuito) della GEOSTAT 2010 summer school

Domattina inizia la GEOSTAT 2010 summer school a Plasencia, Spagna. Per chi volesse seguire via web le lezioni di geostatistici come Roger Bivand, Edzer Pebesma, Gerard Heuvelink, Olaf Conrad, Markus Metz, Victor Olaya e Tom Hengl, dovrebbe essere disponibile un canale web apposito, http://geostat2010.info/Live, dal quale seguire in diretta le lezioni.
Il numero massimo di connessioni in contemporanea sarebbe di soli 60.
Slide, etc? http://geostat2010.info/programme

La pendenza topografica lungo direzioni variabili

Nota: a Novembre 2011 ho pubblicato un post su un plugin Quantum GIS per il calcolo della pendenza, direzionale e massima: http://gisoftw.blogspot.com/2011/11/un-plugin-quantum-gis-per-il-calcolo.html


La pendenza topografica che viene calcolata classicamente nei GIS è la stima della inclinazione della superficie topografica locale, approssimata da un piano. Rappresenta cioè la massima inclinazione di questo piano, corrispondente al gradiente massimo di una superficie. Questo calcolo è permesso dai vari GIS che trattano dati DEM, come Saga, Grass, QuantumGis, ArcView 3 o ArcGis con le rispettive estensioni Spatial Analyst, etc.

Per applicazioni specifiche, possiamo avere bisogno di calcolare la pendenza direzionale, cioè il gradiente della superficie topografica lungo una particolare direzione, compresa tra 0° e 360° rispetto al top della mappa. A mia conoscenza, l'unico software GIS che consente questa operazione è Mirone. Grass consente di calcolare le derivate direzionali lungo le sole direzioni x e y, cioè a 90° e a 0° rispetto al top.

In rari casi, ci può essere necessario calcolare le pendenze di una superficie, topografica o meno, lungo delle direzioni che variano nello spazio. Per questi casi, non sono a conoscenza di alcun software GIS che implementi questa funzionalità. Nel caso specifico, questo tipo di calcolo è necessario per una tesi di dottorato condotta sulle relazioni delle megadune antartiche con i fattori ambientali che le regolano. Interessa calcolare la pendenza delle superficie topografica lungo le direzioni dei venti che variano nello spazio su distanze anche relativamente brevi (ovviamente). Risultati preliminari di questa ricerca sono stati presentati recentemente al congresso IPY di Oslo [1].

Un campo di megadune antartiche, visibile dal mosaico Ramp Radarsat.

Per implementare questa funzionalità, assieme a Maja Radivojevic, la dottoranda chiamata in causa, abbiamo scelto di usare Python. Non nell'ambiente ArcGis o QuantumGis, ma svincolati da ogni particolare software, commerciale o open source che sia.

Il primo quesito per creare questo tipo di algoritmo è: quale metodo di calcolo utilizzare? Ne esistono vari, di complessità variabile. Essendo una prima versione del programma, e essendo le superfici glaciali antartiche in generale piatte, abbiamo scelto una metodologia semplice, che è usata per esempio anche in Surfer e che trovate dettagliata in http://www.malg.eu/pendenzadirezionale.php

Un secondo quesito, quando si analizzano superfici raster, come i DEM, è: quale risoluzione utilizzare? Lo slope, come l'aspect e altri parametri topografici, dipendono dalla risoluzione spaziale usata nei calcoli. Cambiando risoluzione, varia anche il risultato perché questo è relativo alla scala di analisi. La pendenza di una catena montuosa calcolata con una risoluzione di 100 m sarà molto più variabile che se calcolata con una risoluzione di 10 km. Per evitare di dovere ricampionare il DEM di base prima di ogni analisi a differente scala spaziale, è stato considerato un fattore di “smoothing”, che esprime il numero di celle a sinistra e a destra, sopra e sotto, la cella per la quale si calcola lo slope direzionale. Un alto fattore di smoothing considera celle più distanti da quella centrale per i calcoli e quindi il risultato esprime una scala spaziale più ampia rispetto a quella espressa da bassi valori di smoothing.

Esempio di calcolo della pendenza usando uno smoothing factor di 2: vengono utilizzati i valori delle celle a due pixel di distanza in orizzontale e in verticlae dalla cella per la quale si effettua il calcolo.

Chiariti questi due aspetti, la creazione dello script è abbastanza semplice, grazie all'elevato livello di astrazione del linguaggio Python.

Lo script python può essere scaricato e utilizzato in locale da Python.

I dati di partenza richiesti sono:

a) grid delle elevazioni (DEM) in formato ESRI ascii

b) grid delle orientazioni in formato ESRI ascii

c) valore dello smoothing factor

 Il risultato consiste in un grid delle pendenze direzionali espressi in gradi (da 90° a -90°, positivo verso l'alto).

Quanto segue è un esempio di analisi e confronto con i risultati “classici”, su una porzione della superficie glaciale dell'Antartide orientale. Si può notare che la pendenza direzionale secondo direzioni parallele alle orientazioni locali dei venti produce dei risultati alle medie ed alte risoluzioni che differiscono da quelle del metodo classico della massima pendenza.

DEM della zona antartica analizzata.

Orientazioni dei venti utilizzata per il calcolo delle pendenze direzionali mobili.

Mappa delle pendenze direzionali calcolate secondo le orientazioni espresse nella mappa dei venti. Valori positivi indicano pendenze in salita. I valori sono simboleggiati per classi di deviazioni standard dal valore medio.

Risultato del calcolo della pendenza direzionale variabile (valori assoluti) comparato con quello classico ottenuto dai software GIS (massima pendenza). Si nota che mentre le strutture principali non vengono modificate , le strutture di media risoluzione e di dettaglio differiscono. 

Riferimenti bibliografici

[1] Maja Radivojevic, Massimo Frezzotti, Mauro Alberti, 2010. Morphology and Constraining Factors of Antarctic Megadunes. IPY Oslo Conference.

Vettori, non vettoriale

I vettoriali nei GIS sono pane quotidiano. Ma si riferiscono al formato degli oggetti geometrici rappresentati nei GIS e non hanno diretta relazione con i vettori usati in fisica, ingegneria e nelle altre scienze. Se si vogliono trattare i vettori nei GIS, di quali funzioni si dispongono? Di solito, tranne pochi casi, nessuna....

Divergenza, rotore, angoli tra vettori, prodotti scalari e vettoriali?
Possiamo calcolarli o usando delle funzioni da noi scritte, in Python, in Avenue, per esempio, oppure migrando temporaneamente i dati in software come MATLAB. Scomponiamo i vettori in componenti cartesiane conservandoli in due o tre campi della tabella degli attributi, oppure in due o tre grid se consideriamo campi continui, e quindi possiamo applicare le classiche operazioni scalari come addizione, sottrazione, o vettoriali come il prodotto scalare o vettoriale. Se il risultato corrisponde ad un vettore, potrà essere archiviato come prima nelle sue componenti e quando necessario trasformato nelle sue componenti polari.

Maggiori informazioni in questo pdf.

Cressie e Bivand al Spatial Statistics 2011 - 23 - 25 March 2011, Olanda

Su Linkedin viene segnalata la conferenza:

Spatial Statistics 2011, 23 - 25 March 2011, The Netherlands

 

Mapping Global Change - http://www.spatialstatisticsconference.com

Fra gli speaker invitati vi saranno Noel Cressie - autore del famoso Statistics for Spatial Data, Peter Atkinson, Yong Ge, Gilberto Camara, Martin Schlater, Roger Bivand - che si interessa di Geostatistica tramite R.

Come furono calcolati i portolani? Sul Washington Post

Link
http://www.washingtonpost.com/wp-dyn/content/article/2010/05/21/AR2010052104713.html?hpid%3Dtopnews&sub=AR

Verso il Lisp?

Interessante post di Paul Graham, segnalato in mailing list di Python: i linguaggi di programmazione, dal lontano 1958, starebbe tendendo lentamente verso il Lisp, uno degli ultimi casi Python.

http://www.paulgraham.com/icad.html

Mapping Ancient Civilization, in a Matter of Days - NYTimes

http://www.nytimes.com/2010/05/11/science/11maya.html?hpw

PyConf

A Firenze dal 7 al 9 maggio quarta conferenza su Python.
A parte gli abstract degli interventi, non sono presenti video degli interventi di quest'anno, ma si possono vedere alcuni video di quelli degli anni precedenti. Due fra le possibili scelte: quello di Guido van Rossum, BDF di Python, su Goggle App Engine, del 2009,  e di Fabio Rotondo su PyHP, sempre dello stesso anno.

Errori...

La propagazione degli errori nei GIS è un soggetto meno evidenziato e trattato di altri, come le interpolazioni o i cambiamenti di sistemi proiettivi. I dati geografici si portano appresso, esplicitamente o implicitamente, errori ed incertezze di varia natura ed origine, che possono influire sulla qualità dei risultati ottenuti con procedure GIS.

Le operazioni di sovrapposizione vettoriale, per esempio, dipendono dalla correttezza del posizionamento dei limiti geografici e di quella dei valori attribuiti ai vari elementi geografici. Con le sovrapposizioni otteniamo dei risultati che al variare della posizione o per differenti categorie possono avere differente incertezza o entità di errore e quindi influire sulla qualità di decisioni che si prendono supponendo che i risultati siano dappertutto e in ogni caso assolutamente corretti.

Molti aspetti degli errori nei GIS sono ben trattati nel recente testo di Burrough & McDonnell “Principles of Geographical Information Systems” o nel precedente, del solo Burrough, “Principles of Geographical Information Systems for Land Resources Assessment”.

In questo post volevo segnalarvi questa pagina che ho creato su un aspetto particolare, la propagazione degli errori numerici per operazioni analitiche (per esempio somma, moltiplicazione, elevamento a potenza). Sono ricordate le basi teoriche, riprese da Burrough, e per alcuni casi particolari sono descritte le formule per variabili fra loro correlate, assieme a piccole “calcolatrici” (in JavaScript) che permettono di calcolare i risultati per valori specifici. Nasce fondamentalmente da un approfondimento fatto per determinare gli errori associati a dati di flussi glaciali in Antartide, studiati in una tesi di dottorato..

Pagine web dinamiche con Python - la configurazione locale di Apache su Windows

Python permette anche di creare pagine web ed in questo si affianca ad altri linguaggi di scripting come PHP o Ruby. A differenza di PHP e mySQL (un sistema di gestione di database molto diffuso), sono poco diffuse distribuzioni di Apache che integrino Python. Per creare un server locale su cui sperimentare l'uso di Python, è necessario che l'utente si faccia carico, oltre all'installazione di Python, della configurazione di Apache in maniera che riconosca Python. La maniera più semplice per iniziare ad usare Python per il web è utilizzarlo come linguaggio per programmazione CGI (Common Gateway Interface). Per configurare in Windows Apache in maniera tale che riconosca Python come linguaggio CGI, sono necessari pochi settaggi di Apache e degli script Python che si creeranno, ben spiegati in questa pagina del team di EditRocket, un code editor.

Dopo avere installato Python, è necessario configurare Apache.
Si devono effettuare un paio di modifiche del file httpd.conf che si trova nella cartella conf del folder di installazione di Apache.
La prima modifica consiste nella modifica della linea:
  Options Indexes FollowSymLinks
aggiungendo ExecCGI , così da trasformarla in:
  Options Indexes FollowSymLinks ExecCGI

La seconda consiste nel decommentare la riga:
  #AddHandler cgi-script .cg
ed aggiungervi Python come linguaggio, modificandola quindi in:
  AddHandler cgi-script .cgi .py

Effettuate queste due modifiche e riavviato il server Apache, gli script Python che creiamo possono essere usati per generare pagine web dinamiche.

Prendiamo il semplice esempio successivo dal testo di Hans Petter Langtangen su Python, Python Scripting for Computational Science.

Creiamo un semplice Hello-World html file ed uno script Python, a nome hw.py, con questo contenuto:

  #!/Python26/python
  import cgi, math

  # required opening of CGI scripts with HTML output:
  print 'Content-type: text/html\n'

  # extract the value of the variable "r" (in the text field):
  form = cgi.FieldStorage()
  r = form.getvalue('r');

  s = str(math.sin(float(r)))
  print 'Hello, World! The sine of %s equals %s' % (r,s)


Notate la prima linea:
  #!/Python26/python

Essa fornisce il percorso all'eseguibile di Python. L'esempio sovrastante si riferisce ad una installazione di Python 2.6 nel folder: c:\Python26.
Se aveste installato Python 2.5 nel folder c:\Programmi\Python25, la prima linea sarebbe:
  #!/Programmi/Python25/python

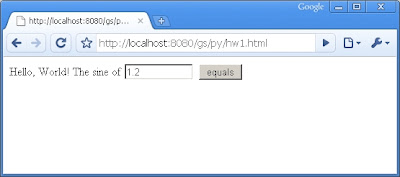
Il file html Hello World, lanciato dal server locale, apparirà così:

e utilizzando lo script Python genererà una pagina web dinamica che ci illustra il valore del seno del numero inserito nella finestra: