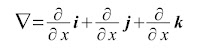Estensioni per ArcView 3?

ArcView 3, anche se scomparso dall'orizzonte dello sviluppo e vendite di ESRI, è presumibilmente ancora utilizzato in varie occasioni, per esempio per visualizzare coverage o grid in formato ESRI, per verificare il sistema proiettivo di un livello che ArcGis colloca in una posizione molto lontana da quella che ci aspetteremmo o anche per operazioni standard come digitalizzazioni e simili. Uno dei suoi fattori di successo è l'abbondante numero di estensioni, prevalentemente libere, che sono state sviluppate e che non sempre sono state tradotte in versioni per ArcGis. In questo post elenco alcune estensioni free per ArcView 3.x che possono essere utili, particolarmente nel settore delle Scienze della Terra.

Queste estensioni si possono suddividere in due categorie principali, per processamenti di dati vettoriali e per processamenti raster.

Nel primo gruppo due fra le più utili sono XTools ed EditTools.

Il primo è una versione free, scaricabile da http://arcscripts.esri.com/details.asp?dbid=11526 , creata da Mike Delaune. Permette di effettuare geoprocessing su livelli vettoriali (per es. clip, unione, intersezione) ed anche di convertire le geometrie da/a puntuale-lineare-poligonale e da geometrie raggruppate a singole (p.e. da regioni a poligoni individuali). Consente inoltre operazioni di visualizzazione delle caratteristiche e delle statistiche di tabelle descrittive di livelli vettoriali.

EditTools (http://www.ian-ko.com/ ) fornisce le stesse funzionalità geometriche di XTools, aggiungendone varie altre, come quelle dedicate alla creazione di poligoni di Thiessen, al calcolo del convex-hull e alla creazione di livelli 3D (anche come TIN).

Per quanto riguarda i dati raster, ma anche per processamenti vettoriali, una delle più interessanti suite di strumenti è quella fornita da Jenness Enterprises (http://www.jennessent.com/arcview/arcview_extensions.htm). Alcuni di questi strumenti sono stati anche tradotti per ArcGis. Qui accennerò brevemente solo ad alcune dedicate a dati raster. Nota: in generale richiedono la disponibilità dell'estensione ESRI Spatial Analyst.

Grid Tools permette di geoprocessare grid con operazioni di clip, mosaicatura e simili, di derivare statistiche descrittive e di applicare scale di colori efficaci e gradevoli. Con Directional Slope si può calcolare la pendenza lungo direzioni costanti. Grid and Theme Regression consente di analizzare le relazioni statistiche spaziali tra più livelli, raster e vettoriali.

Un ultimo tool che consiglio è Profile Extractor (http://www.ian-ko.com/ ), che permette di creare profili verticali a partire da livelli grid, anche più di uno in una stessa sezione. Questi profili possono poi essere esportati, anche come dati numerici per essere utilizzati in altri software.

Adding a GUI to a Python script

We can quite easily add a GUI to a Python script by using the PyQt module (http://wiki.python.org/moin/PyQt ).

As an example, I use a command-line script described in a previous post (in Italian): La pendenza topografica lungo direzioni variabili (http://gisoftw.blogspot.com/2010/06/la-pendenza-topografica-lungo-direzioni.html). This script calculates the directional slope of a DEM along orientations defined in an accompanying grid. These orientations typically vary in space and can represent for instance wind directions or glacial flows.

A more recent version of this script has also a GUI, obtained by changing just a few tens of code lines and without the need of Qt Designer (http://qt.nokia.com). In this last version, the GUI manages the definition of the input files and calculates the output slope grids according to two methods: a central differences method and Horn (1981) method. One can look at http://www.malg.eu/opensoftware/dem/directionalslope.php for additional details, download and a case study.

A valuable book for learning GUI scripting in Python is Rapid GUI Programming with Python and Qt, by Mark Summerfield (http://www.qtrac.eu/pyqtbook.html ). As a development environment, Python(x,y) (http://code.google.com/p/pythonxy) has all the required dependencies, so that one can start coding GUI without additional installations.

'Copiapó', i.e. QuantumGIS 1.6.0

The developers of QuantumGIS have just announced the release of QuantumGIS 1.6.0, named 'Copiapó. The previous one was released less than 4 months ago.
For more info see:
 http://blog.qgis.org/node/146

Conversions from points to lines: which methods?

(english version of post “Conversione da punti a linee: come?”, published 2010-11-09)


One of the first concepts presented in GIS courses is that vector data have point, line and polygon geometries. And we can switch between them without significant problems. However, such changes can be problematic in practice.


The actual case? I have a polygon layer of the geology in an area of the Nera Valley (Umbria, east of Foligno). I want to extract faults into a new line layer, using the contacts that already exist between the geological formation and geological formation (I ignore the faults developed entirely inside a formation). By converting polygon to line geometries, I face two main drawbacks. Line editing to delete unwanted stratigraphic limits is error prone. The latter is that line orientations are often inconsistent along a same fault.


In practice, it is more convenient to convert the lines into points, clear all unnecessary points, assign a common identifier to all the points representing a single fault, and then convert the geometry from point to line, based on fault identifiers.

While point editing is just boring, the last step can be tricky. I try with some software tools, and the result is not the expected one. There is an abundance of redundant lines, connecting points that should not be connected. It may depend on the inconsequential order of the original lines and also the presence of duplicated points generated by the polygon-to-line conversion.

Good opportunity for programming with Python. I try to create a tool ensuring proper processing ofpoint ? line conversion. Apart from removing duplicated points, we need a successful logic of conversion point ? line. It could be quite straightforward, considering that fault traces have an almost straight alignment. Therefore, a tentative algorithm for a single fault could consist in finding the two extremes of the fault trace, then, starting from an extreme, connect to each point the closest, unused one.


Can a straightforward strategy as the one depicted convert effectively points to elementary linear geometries? How to find quickly, from the execution time point of view, the most distant points, or vice versa the closest ones?


The second question can be approached via a distance matrix, which stores the distances between each point couple. So the largest distance can be easily picked, or alternatively the shortest distance between a point and a set of other points. Assuming that the largest distance is due to the two fault ends, we can find them. From one of the ends, we can then select the shortest distance with another point and connect the two points. Then, we mark the starting point as used (i.e., set all its distances to infinity) and re-apply the same logic until we use all the points. For this processing, the numpy Python module is suitable.


The answer to the first question is positive, at least in this case. This simple strategy allows an accurate conversion to line geometry. Obviously for more complex and general cases, a more sophisticated strategy would be needed.

The Python script and the used data are available in this zipped file. Input and output data format is shapefile. Required Python modules are numpy and ogr: I used Python (x, y), which already incorporates these modules. The FWTools software has the older Numeric module instead of the recent numpy. Therefore, the script should not work in FWTools, or you should modify from numpy to Numeric terminology. Other Python distributions with numpy ogr and could work without problems. The program run from the shell with the following command line:


python pt2line_05.py par.txt


where pt2line_05.py is the script name and par.txt is the text file that contains the parameters (name of the input point shapefile, name of the output line shapefile and name of the field that contains the numeric identifier of each line). An example is: 
flt_pts.shp
flt_lines.shp
flt_id

Conversione da punti a linee: come?

(english version: http://gisoftw.blogspot.com/2010/11/conversions-from-points-to-lines-which.html)

Uno dei primi concetti che vengono illustrati nei corsi GIS per descrivere i dati vettoriali è che esistono geometrie puntuali, lineari e poligonali. E che è possibile passare dall'una all'altra geometria. Tentare di metterlo in pratica può riservare sorprese, come si impara con l'esperienza.

Qual'è il caso specifico? Ho un livello poligonale, che rappresenta la geologia in un settore della Valnerina (Umbria, ad est di Foligno). Voglio isolare le faglie in un nuovo livello lineare, partendo dai contatti geologici che sono già presenti tra formazione e formazione geologica (trascuro le faglie che si sviluppano esclusivamente all'interno di una stessa formazione).

Convertendo il livello da poligonale a lineare mi presenta tutta una serie di problemi: i limiti possono avere significato sia di faglia sia di limite stratigrafico. I loro identificativi non sono coerenti. I versi delle linee non sono costanti lungo una stessa faglia. L'eliminazione dei limiti lineari che non interessano è macchinoso e soggetto ad errori.

In pratica, è più comodo retrocedere i dati a puntuali, cancellare tutti i punti inutili, attribuire un identificativo comune a tutti i punti che rappresentano una singola faglia, e poi trasformare tutti in lineare in base all'identificativo.

Ma non è così banale l'ultimo passaggio (quelli precedenti sono solo noiosi). Provo con alcuni strumenti di vari software, ed i risultati lasciano a desiderare. Linee ridondanti, che collegano punti che dovrebbero essere sconnessi, e simili amenità. Può dipendere dall'ordine, non sequenziale e con versi variabili, dei punti, ed anche dal fatto che purtroppo i punti si sono anche duplicati e triplicati nella conversione poligonale → lineare → puntuale.

Buona occasione per programmare con Python, tentando di creare uno strumento che risparmi ulteriori grattacapi effettuando correttamente la trasformazione punti → linee. A parte la cancellazione dei duplicati, serve una logica di conversione punto → linea, magari anche semplificata considerando che le tracce di faglie hanno uno sviluppo grosso modo rettilineo, senza particolari zig-zag interni. Può essere quella di trovare le due estremità della faglia, poi di partire da un estremo e man mano collegare ad ogni punto quello più vicino che non è ancora stato utilizzato.

Può essere sufficiente una strategia così semplice per dati di faglia?

E come trovare in maniera veloce, dal punto di vista dei tempi di esecuzione, i punti più distanti o viceversa quelli fra loro più vicini?

La seconda questione può essere risolta calcolando una matrice delle distanze, che conserva per ogni punto la distanza dai punti dell'intero set. Così si rintracciano subito i due punti più distanti fra loro, e nell'assunzione che rappresentino gli estremi della faglia, se ne sceglie uno e da questo si sceglie via via il punto più vicino, marcando come già usato il precedente (nella matrice delle distanze si settano i suoi valori in riga e in colonna ad infinito), fino ad esaurire i valori di distanza non infiniti nella matrice. Naturalmente, dopo avere scelto la distanza massima, i valori di distanza nulla di ogni punto con se stesso vengono resi inoffensivi trasformandoli in infinito. Il modulo Numpy di Python è adatto per questo genere di elaborazioni.

La risposta alla prima questione, almeno nel mio caso, è stata positiva. Una strategia così semplice permette di ottenere una geometria lineare corretta che rispetta gli andamenti delle faglie. Ovviamente su dati più complessi occorrerebbero strategie più sofisticate, per esempio per trattare i casi in cui non si selezionano correttamente gli estremi.

Lo script Python e i dati reali usati sono disponibili in questo file zippato. I moduli richiesti sono numpy e ogr: io ho effettuato le elaborazioni in Python(x,y), che incorpora già questi moduli. In FWTools numpy non è presente, ma solo il suo predecessore Numeric, e quindi questo modulo non funzionarebbe a meno di convertire la sintassi numpy in numeric. Altre distribuzioni osgeo con Python, Numpy e ogr dovrebbero invece andare bene.

Il programma si lancia dalla shell con la linea di comando:

python pt2line_05.py par.txt

dove pt2line_05.py è il nome dello script e par.txt è quello del file testuale che contiene i parametri (nome dello shapefile puntuale di input, dello shapefile lineare di output, del campo che contiene l'identificativo numerico di ogni linea), per esempio: 

flt_pts.shp

flt_lines.shp

flt_id

Due eventi "open gis" a breve in Italia

Sono:
GFOSS DAY 2010 - Foligno (Pg) - 18 e 19 Novembre 2010: http://www.gfoss.it/drupal/gfossday2010
PgDay 2010 - Roma - 10 Dicembre 2010: http://2010.pgday.it/.

Le registrazioni al secondo evento, dedicato a PostgreSQL, si sono aperte oggi, 8 Novembre.

Antartide e GIS

E' un continente quasi sempre lontano dai riflettori della cronaca. Viene citato talvolta quando qualche grande iceberg si distacca dalle sue piattaforme glaciali, evento magari presentato come "diretta conseguenza" del riscaldamento globale. La scienza invece ha gli occhi puntati su questo continente da più di un secolo. La ricerca  ha bisogno di un sistema di riferimento cartografico solido, oltre che dati per studiarlo, per esempio immagini satellitari e dati cartografici.
Quali sono i sistemi cartografici usati e quali i dati di base disponibili?
Tra i ricercatori il sistema più usato, soprattutto se si studia l'intero continente, è il Polare Stereografico. Il parallelo standard è il -71°, ovvero 71°S. Il datum, come al solito, è il WGS84. Ovviamente questo stesso sistema può essere usato specularmente per le zone polari settentrionali.
Questo sistema è quello usato per la più comprensiva raccolta di dati cartografici a scala dell'intera Antartide,  l'Antartic Digital Database: http://www.add.scar.org:8080/add/. Questo database cartografico è open, salvo registrazione preliminare. E' stato supervisionato dal British Antarctic Survey (BAS) e raccoglie, suddivisi in una serie di tiles (vista la vasta superficie del continente), una serie di livelli che vanno dalle curve di livello, alle colonie di animali (pinguini, petrelle e simili), alle linee di flusso glaciali. E' di qualità buona, anche se localmente possono essere presenti alcune incongruenze o i dati possono non essere aggiornati, per esempio dove le lingue glaciali si sono modificate recentemente. Le fonti dei dati sono infatti i prodotti cartografici di svariate nazioni e su lunghi periodi di tempo, il che giustifica le variazioni di qualità ed aggiornamento nonostante il tentativo di uniformazione praticato sotto la guida del BAS.
Accoppiabili a questi dati vi sono i mosaici satellitari a scala continentale: due classici sono il MOA (MODIS Mosaic of Antartica): http://nsidc.org/data/moa/index.html,  ed il RAMP Radarsat: http://nsidc.org/data/nsidc-0103.html. Entrambi sono monobanda a scala di grigi, a 125 m di risoluzione nominale e già georiferiti in Polare Stereografica. Mentre il MOA deriva da sensori nell'ottico, il RAMP si basa su un sensore radar (quindi con le situazioni di spostamento apparente delle zone rilevate tipiche di questa metodologia).

Nelle due immagini sottostanti è visualizzata la lingua glaciale Drygalski, lunga circa 100 km, prima del suo impatto con l'iceberg B15A (avvenuto ad Aprile 2005, http://www.esa.int/esaCP/SEMEGLW797E_index_0.html). La prima immagine è RAMP-Radarsat, la seconda MOA.

Più recente è il Landsat Image Mosaic of Antarctica (LIMA): http://lima.usgs.gov/, che deriva da immagini Landsat con una risoluzione nominale di 30 m e viene redistribuito ricampionato a 240 m di risoluzione in formato jp2.
Oltre a questo è possibile anche scaricare le immagini Landsat. Ma con la recente liberalizzazione dei dati Landsat, forse è più semplice e ricco scegliere le immagini da scaricare dal sito glovis: http://glovis.usgs.gov/.

20 Ottobre 2010 - Prima Giornata Mondiale della Statistica - World Statistics Day

La Prima Giornata Mondiale della Statistica. Indetta dalle Nazioni Unite.
Il link ufficiale: http://unstats.un.org/unsd/wsd/
In Italia l'Istat si occupa dell'organizzazione:  http://www.istat.it/istat/eventi/2010/giornata_mondiale_statistica/
organizzando anche il barcamp Sharing data & Statistical knowledge.
Uno dei tavoli del barcamp sarà dedicato ai Sistemi Informativi Geografici, con "facilitatore" Sandro Furieri, presidente Gfoss. 
E' previsto uno streaming: http://video2.caspur.it/barcamp/streaming.html

E' morto Benoit Mandelbrot, il padre dei frattali

Anche se nei GIS il concetto di frattale è ancora poco applicato, è stato un concetto rivoluzionario per l'economia, le scienze fisiche, la geomorfologia (reticolati idrografici e topografie frattali), oltre che anche in campo artistico.
Il padre di questa teoria, Benoit Mandelbrot, polacco emigrato in Francia e poi negli USA, è morto oggi.

http://www.nytimes.com/2010/10/17/us/17mandelbrot.html?_r=1&hp

Spostamenti nei ghiacciai

Una coppia di immagini satellitari o aeree di una zona, riprese in due periodi differenti, può raccontare molto sulle variazioni avvenute in quell'arco di tempo. Mentre per riprese a latitudini basse e intermedie, le variazioni potranno riguardare la vegetazione, i cambiamenti urbani o i movimenti del suolo, per le alte latitudini entra in gioco la dinamica della criosfera. Si potranno così monitorare gli spostamenti lungo i ghiacciai, le variazioni di estensione del ghiaccio marino o delle fronti di ice shelves (ghiaccio continentale galleggiante sul mare). Considerando la dinamica dei flussi glaciali, dalle immagini teleriprese è possibile determinare gli spostamenti lungo i ghiacciai anche nell'arco di tempo di pochi anni. Vari sono i metodi di determinazione. Per zone che presentano solo spostamenti senza significative rotazioni e deformazioni interne, è possibile usare un software open source, creato per la determinazione dei flussi glaciali. Si tratta di Imcorr, del quale trovate i riferimenti in http://nsidc.org/data/velmap/imcorr.html. L'articolo che lo presenta è Scambos et al. (1992). Bibliografia addizionale su Imcorr è presente in http://www.geo.unizh.ch/~kaeaeb/glims/glims.html#Anchor-Glacier-23240

E' un programma a linee di comando, quindi privo di interfaccia grafica, che può essere usato nei sistemi Unix e Linux o Linux-like, come Cygwin inWindows. Imcorr è basato sui linguaggi C e Fortran. C gestisce l'input e l'output dei dati e dei risultati, oltre al passaggio dei dati verso le subroutine Fortran che effettuano i calcoli. La determinazione degli spostamenti presumibili avviene con metodi di cross-correlation a loro volta basate su trasformate di Fourier. Il requisito fondamentale per i dati di input di Imcorr è che le due immagini da comparare siano fra loro già co-registrate ed abbiano le stesse dimensioni (uguale numero di righe e di colonne). La scelta dei parametri ottimali di dimensione delle sotto-immagini entro cui effettuare la ricerca è forse la parte più gravosa dell'intera procedura di elaborazione.

Un esempio di applicazione di Imcorr a dati satellitari Landsat è rappresentato dalla ricerca di I. Pino sui ghiacciai antartici della Terra Vittoria, in Antartide, reperibile all'indirizzo http://amsdottorato.cib.unibo.it/1177/

Un'altra tesi di dottorato basata su derivazione di velocità di flussi glaciali per zone dell'Antartide orientale è quella di D. Biscaro, il cui abstract è scaricabile da http://www.mna.it/italiano/Didattica/dott_polare/Tesi_abstract/Biscaro_XXI_2010.pdf

Too many elevations?

Having to manage elevation data sets with hundreds of thousands or more of records is becoming a standard, but not easy task, even with the most powerful GIS software. This can be due both to the difficulty of interpolating large data sets, and to irregular spatial distributions of data that can lead to produce DEM with artifacts, particularly evident when deriving morphological parameters (slope, aspect and so on).

As a practical example, we consider a data set of elevations for a sector of Antarctica, deriving from ICESat satellite data measured over a period from 2003 to 2008. It consists of nearly 2,800,000 data showed in the map below. Data density along satellite tracks is high (every 172 meters), with several different tracks nearly covering each other, while the spacing across track is much higher, for instance in the top-left of the map this spacing is between five and ten kilometers. In many subareas of this zone, the local topography presents periodic height variations (not visible in this map), due to the presence of glacial megadune fields. Megadunes have wavelengths of several kilometers, amplitudes of several meters and lateral continuity of tens of km. Clearly, DEM deriving from these data are much more affected by local structures in correspondence of tracks.

A possible remedy for this situation is the use of spatial filters that reduce and uniform as much as possible the data density. A straightforward methodology is the use of a grid-based filter to the values of height. For each grid cell, a filter calculates a single height value, based on some functions that process the records falling in the cell. In general algorithms calculate the average of records, whether of height or other analysed properties. Usually the position attributed to the calculated value is at the cell center. Although results calculated in this way can be considered fundamentally correct, we note three negative aspects: the use of the mean introduces a smoothing of the values; erroneous data affects the average value; positioning the resulting value at the cell center can change the variographic properties of the data set.

I present a short program in C + + command line (without GUI), which filters the data in a grid, determines the median values (when there are three or more values) and preserves the original location of the median value. Program (compiled with CodeBlocks in Windows), source code and parameter and elevation example files are available here. Session parameters are in a text file (example: 'param.txt'), and the program loads this file to read the parameters. This program processes ICESat data, but obviously it can be applied to any elevation data, provided that they share the same, basic textual input structure, i.e. with space-separated record id (integer), x, y, z, structured in a column format (see example in file 'elevations.txt'). 

The use of the median avoids the smoothing of elevations, as well as reducing the impact of inaccurate, extreme values. The median record maintains its original position, obviously falling within the borders of the cell in question. 

The algorithm creates two textual outputs. The former is a grid in the ESRI ASCII format that stores the number of records in each grid cell. Open source GIS like Saga or Quantum Gis can read this format. The latter is a file in table format that stores the median elevation values together with the original spatial location of the median value.

Running this program on the previous Antarctic data set with 1 km cell size reduces the amount of data to 70,988 from 2,783,551, i.e. with a 97.4% reduction of the data number, without substantially changing the available data structure, as the map below, representing the filtered data, evidences.

As another example, if we use a 250 meters cell size, the data number reduces to 444,532 (about 16% of the original amount). The filter also eliminates many spikes in the frequency histogram (below, blue: original data, orange: filtered data), probably corresponding to artifacts related the track oversampling of local areas, since no natural reasons for their existence.

Mappa delle offerte di lavoro GIS

The GIS Jobs Clearinghouse Map rappresenta in mappa offerte di lavoro GIS:
http://www.gjc.org/map.html.

E basandosi sulla mappa l'Europa non appare brillare...

GoogleMars

Istruzioni per visitare Marte.

Get Flash to see this player.

Operatori vettoriali nei GIS: il gradiente

Nei GIS i procedimenti e le visualizzazioni di dati vettoriali non sono molto diffuse, fatto salvo il caso del calcolo delle pendenze topografiche. I GIS calcolano implicitamente un campo vettoriale, tramite due distinti campi scalari, l'esposizione (aspect) e la pendenza (slope), che esprimono rispettivamente l'orientazione della massima inclinazione rispetto al nord della mappa ed il valore di inclinazione rispetto al piano orizzontale.

Questo campo vettoriale corrisponde al gradiente di un campo scalare, l'elevazione. Il gradiente viene calcolato applicando ad una superficie scalare ϕ(x,y,z), supposta continua e derivabile in ogni punto, l'operatore differenziale vettoriale nabla:

Nel caso di una superficie topografica la superficie è funzione di due soli variabili spaziali, x e y, per cui z = ϕ(x,y) e il suo gradiente vale:

Il risultato è un campo vettoriale bi-dimensionale su un piano orizzontale. Per ogni punto del dominio spaziale, il vettore orizzontale punta nella direzione di massima pendenza della topografia ed ha un modulo proporzionale alla pendenza di questa.

Con linguaggi di scripting e software open source è possibile calcolare e visualizzare questo campo vettoriale come entità singola, non scissa in esposizione e pendenza. In questo post vediamo un esempio che si basa su Python per il processamento e su ParaView per la visualizzazione.

Dato che nella realtà le superfici topografiche non sono rappresentate da superfici analitiche ma da misure discrete nello spazio, una implementazione del calcolo del gradiente si deve basare su dati discreti, archiviati in formati come il raster a celle quadrate. Esistono varie formulazioni per il calcolo del gradiente nei GIS. Quella di base, implementata per esempio in Surfer, calcola i due gradienti lungo le direzioni x e y come differenze discrete tra i valori delle due celle contigue alla cella centrale.

dz/dx = [ Elev(i, j + 1) - Elev(i, j - 1) ] / 2*cell_size

dz/dy = [ Elev(i - 1, j) - Elev(i + 1, j) ] / 2*cell_size

In questo script Python, modificato da quello precedentemente creato per il calcolo della pendenza lungo direzioni variabili nello spazio, questa formulazione fornisce la possibilità di definire la distanza delle due celle laterali o verticali dalla cella centrale, in maniera tale da utilizzarlo come un fattore di smoothing che regola la risoluzione effettiva per la quale il gradiente è calcolato.

dz/dx = [ Elev(i, j + n) - Elev(i, j - n) ] / 2*n*cell_size

dz/dy = [ Elev(i - n, j) - Elev(i + n, j) ] / 2*n*cell_size

Il valore rappresenta il numero di celle a sinistra e a destra per la differenza lungo le x, o sopra e sotto per le y, utilizzate nel calcolo (esempio con smoothing factor uguale a 2 in figura sottostante).

Lo script Python calcola le componenti lungo i due assi a partire da un file ascii nel formato ESRI grid e le salva, assieme ai valori di elevazione, in un file ascii nel formato vtk (legacy vtk format). Col software ParaView è possibile visualizzare ed elaborare questi dati scalari e vettoriali. ParaView non è particolarmente intuitivo come utilizzo, ma con alcuni tentativi si riesce a capire quali sono le funzioni di base utili per visualizzare dati.

Usiamo dati liberi dello Shuttle Radar Topography Mission (SRTM2), con risoluzione nominale di 90 m, del lago di Bolsena, nel Lazio.

Il modulo del campo vettoriale viene calcolato automaticamente da ParaView, a partire dalle sue componenti.

Queste stesse componenti sono visualizzabili e rendono bene l'andamento morfologico della superficie, meno evidente dalle immagini satellitari, e che consiste in caldere di varie dimensioni, fra loro coalescenti. I valori positivi delle componenti indicano salite spostandosi da ovest verso est, nel caso del gradiente lungo le x, e dall'alto verso il basso, per il gradiente lungo le y.

Ed infine, il campo vettoriale può essere rappresentato utilizzando una serie di glifi che indicano l'orientazione dei vettori ed il loro modulo, sempre a partire dalle singole componenti cartesiane. Ovviamente anche nei GIS è possibile rappresentare questa informazione, ma occorre calcolare il valore angolare dell'orientazione ed utilizzarlo come campo di rotazione del glifo. Nella figura sottostante è rappresentato il campo vettoriale per un settore limitato della zona considerata.

Lunedì 28 giugno: Live broadcast (gratuito) della GEOSTAT 2010 summer school

Domattina inizia la GEOSTAT 2010 summer school a Plasencia, Spagna. Per chi volesse seguire via web le lezioni di geostatistici come Roger Bivand, Edzer Pebesma, Gerard Heuvelink, Olaf Conrad, Markus Metz, Victor Olaya e Tom Hengl, dovrebbe essere disponibile un canale web apposito, http://geostat2010.info/Live, dal quale seguire in diretta le lezioni.
Il numero massimo di connessioni in contemporanea sarebbe di soli 60.
Slide, etc? http://geostat2010.info/programme

La pendenza topografica lungo direzioni variabili

Nota: a Novembre 2011 ho pubblicato un post su un plugin Quantum GIS per il calcolo della pendenza, direzionale e massima: http://gisoftw.blogspot.com/2011/11/un-plugin-quantum-gis-per-il-calcolo.html


La pendenza topografica che viene calcolata classicamente nei GIS è la stima della inclinazione della superficie topografica locale, approssimata da un piano. Rappresenta cioè la massima inclinazione di questo piano, corrispondente al gradiente massimo di una superficie. Questo calcolo è permesso dai vari GIS che trattano dati DEM, come Saga, Grass, QuantumGis, ArcView 3 o ArcGis con le rispettive estensioni Spatial Analyst, etc.

Per applicazioni specifiche, possiamo avere bisogno di calcolare la pendenza direzionale, cioè il gradiente della superficie topografica lungo una particolare direzione, compresa tra 0° e 360° rispetto al top della mappa. A mia conoscenza, l'unico software GIS che consente questa operazione è Mirone. Grass consente di calcolare le derivate direzionali lungo le sole direzioni x e y, cioè a 90° e a 0° rispetto al top.

In rari casi, ci può essere necessario calcolare le pendenze di una superficie, topografica o meno, lungo delle direzioni che variano nello spazio. Per questi casi, non sono a conoscenza di alcun software GIS che implementi questa funzionalità. Nel caso specifico, questo tipo di calcolo è necessario per una tesi di dottorato condotta sulle relazioni delle megadune antartiche con i fattori ambientali che le regolano. Interessa calcolare la pendenza delle superficie topografica lungo le direzioni dei venti che variano nello spazio su distanze anche relativamente brevi (ovviamente). Risultati preliminari di questa ricerca sono stati presentati recentemente al congresso IPY di Oslo [1].

Un campo di megadune antartiche, visibile dal mosaico Ramp Radarsat.

Per implementare questa funzionalità, assieme a Maja Radivojevic, la dottoranda chiamata in causa, abbiamo scelto di usare Python. Non nell'ambiente ArcGis o QuantumGis, ma svincolati da ogni particolare software, commerciale o open source che sia.

Il primo quesito per creare questo tipo di algoritmo è: quale metodo di calcolo utilizzare? Ne esistono vari, di complessità variabile. Essendo una prima versione del programma, e essendo le superfici glaciali antartiche in generale piatte, abbiamo scelto una metodologia semplice, che è usata per esempio anche in Surfer e che trovate dettagliata in http://www.malg.eu/pendenzadirezionale.php

Un secondo quesito, quando si analizzano superfici raster, come i DEM, è: quale risoluzione utilizzare? Lo slope, come l'aspect e altri parametri topografici, dipendono dalla risoluzione spaziale usata nei calcoli. Cambiando risoluzione, varia anche il risultato perché questo è relativo alla scala di analisi. La pendenza di una catena montuosa calcolata con una risoluzione di 100 m sarà molto più variabile che se calcolata con una risoluzione di 10 km. Per evitare di dovere ricampionare il DEM di base prima di ogni analisi a differente scala spaziale, è stato considerato un fattore di “smoothing”, che esprime il numero di celle a sinistra e a destra, sopra e sotto, la cella per la quale si calcola lo slope direzionale. Un alto fattore di smoothing considera celle più distanti da quella centrale per i calcoli e quindi il risultato esprime una scala spaziale più ampia rispetto a quella espressa da bassi valori di smoothing.

Esempio di calcolo della pendenza usando uno smoothing factor di 2: vengono utilizzati i valori delle celle a due pixel di distanza in orizzontale e in verticlae dalla cella per la quale si effettua il calcolo.

Chiariti questi due aspetti, la creazione dello script è abbastanza semplice, grazie all'elevato livello di astrazione del linguaggio Python.

Lo script python può essere scaricato e utilizzato in locale da Python.

I dati di partenza richiesti sono:

a) grid delle elevazioni (DEM) in formato ESRI ascii

b) grid delle orientazioni in formato ESRI ascii

c) valore dello smoothing factor

 Il risultato consiste in un grid delle pendenze direzionali espressi in gradi (da 90° a -90°, positivo verso l'alto).

Quanto segue è un esempio di analisi e confronto con i risultati “classici”, su una porzione della superficie glaciale dell'Antartide orientale. Si può notare che la pendenza direzionale secondo direzioni parallele alle orientazioni locali dei venti produce dei risultati alle medie ed alte risoluzioni che differiscono da quelle del metodo classico della massima pendenza.

DEM della zona antartica analizzata.

Orientazioni dei venti utilizzata per il calcolo delle pendenze direzionali mobili.

Mappa delle pendenze direzionali calcolate secondo le orientazioni espresse nella mappa dei venti. Valori positivi indicano pendenze in salita. I valori sono simboleggiati per classi di deviazioni standard dal valore medio.

Risultato del calcolo della pendenza direzionale variabile (valori assoluti) comparato con quello classico ottenuto dai software GIS (massima pendenza). Si nota che mentre le strutture principali non vengono modificate , le strutture di media risoluzione e di dettaglio differiscono. 

Riferimenti bibliografici

[1] Maja Radivojevic, Massimo Frezzotti, Mauro Alberti, 2010. Morphology and Constraining Factors of Antarctic Megadunes. IPY Oslo Conference.

Vettori, non vettoriale

I vettoriali nei GIS sono pane quotidiano. Ma si riferiscono al formato degli oggetti geometrici rappresentati nei GIS e non hanno diretta relazione con i vettori usati in fisica, ingegneria e nelle altre scienze. Se si vogliono trattare i vettori nei GIS, di quali funzioni si dispongono? Di solito, tranne pochi casi, nessuna....

Divergenza, rotore, angoli tra vettori, prodotti scalari e vettoriali?
Possiamo calcolarli o usando delle funzioni da noi scritte, in Python, in Avenue, per esempio, oppure migrando temporaneamente i dati in software come MATLAB. Scomponiamo i vettori in componenti cartesiane conservandoli in due o tre campi della tabella degli attributi, oppure in due o tre grid se consideriamo campi continui, e quindi possiamo applicare le classiche operazioni scalari come addizione, sottrazione, o vettoriali come il prodotto scalare o vettoriale. Se il risultato corrisponde ad un vettore, potrà essere archiviato come prima nelle sue componenti e quando necessario trasformato nelle sue componenti polari.

Maggiori informazioni in questo pdf.

Cressie e Bivand al Spatial Statistics 2011 - 23 - 25 March 2011, Olanda

Su Linkedin viene segnalata la conferenza:

Spatial Statistics 2011, 23 - 25 March 2011, The Netherlands

 

Mapping Global Change - http://www.spatialstatisticsconference.com

Fra gli speaker invitati vi saranno Noel Cressie - autore del famoso Statistics for Spatial Data, Peter Atkinson, Yong Ge, Gilberto Camara, Martin Schlater, Roger Bivand - che si interessa di Geostatistica tramite R.

Come furono calcolati i portolani? Sul Washington Post

Link
http://www.washingtonpost.com/wp-dyn/content/article/2010/05/21/AR2010052104713.html?hpid%3Dtopnews&sub=AR

Verso il Lisp?

Interessante post di Paul Graham, segnalato in mailing list di Python: i linguaggi di programmazione, dal lontano 1958, starebbe tendendo lentamente verso il Lisp, uno degli ultimi casi Python.

http://www.paulgraham.com/icad.html

Mapping Ancient Civilization, in a Matter of Days - NYTimes

http://www.nytimes.com/2010/05/11/science/11maya.html?hpw

PyConf

A Firenze dal 7 al 9 maggio quarta conferenza su Python.
A parte gli abstract degli interventi, non sono presenti video degli interventi di quest'anno, ma si possono vedere alcuni video di quelli degli anni precedenti. Due fra le possibili scelte: quello di Guido van Rossum, BDF di Python, su Goggle App Engine, del 2009,  e di Fabio Rotondo su PyHP, sempre dello stesso anno.

Errori...

La propagazione degli errori nei GIS è un soggetto meno evidenziato e trattato di altri, come le interpolazioni o i cambiamenti di sistemi proiettivi. I dati geografici si portano appresso, esplicitamente o implicitamente, errori ed incertezze di varia natura ed origine, che possono influire sulla qualità dei risultati ottenuti con procedure GIS.

Le operazioni di sovrapposizione vettoriale, per esempio, dipendono dalla correttezza del posizionamento dei limiti geografici e di quella dei valori attribuiti ai vari elementi geografici. Con le sovrapposizioni otteniamo dei risultati che al variare della posizione o per differenti categorie possono avere differente incertezza o entità di errore e quindi influire sulla qualità di decisioni che si prendono supponendo che i risultati siano dappertutto e in ogni caso assolutamente corretti.

Molti aspetti degli errori nei GIS sono ben trattati nel recente testo di Burrough & McDonnell “Principles of Geographical Information Systems” o nel precedente, del solo Burrough, “Principles of Geographical Information Systems for Land Resources Assessment”.

In questo post volevo segnalarvi questa pagina che ho creato su un aspetto particolare, la propagazione degli errori numerici per operazioni analitiche (per esempio somma, moltiplicazione, elevamento a potenza). Sono ricordate le basi teoriche, riprese da Burrough, e per alcuni casi particolari sono descritte le formule per variabili fra loro correlate, assieme a piccole “calcolatrici” (in JavaScript) che permettono di calcolare i risultati per valori specifici. Nasce fondamentalmente da un approfondimento fatto per determinare gli errori associati a dati di flussi glaciali in Antartide, studiati in una tesi di dottorato..

Pagine web dinamiche con Python - la configurazione locale di Apache su Windows

Python permette anche di creare pagine web ed in questo si affianca ad altri linguaggi di scripting come PHP o Ruby. A differenza di PHP e mySQL (un sistema di gestione di database molto diffuso), sono poco diffuse distribuzioni di Apache che integrino Python. Per creare un server locale su cui sperimentare l'uso di Python, è necessario che l'utente si faccia carico, oltre all'installazione di Python, della configurazione di Apache in maniera che riconosca Python. La maniera più semplice per iniziare ad usare Python per il web è utilizzarlo come linguaggio per programmazione CGI (Common Gateway Interface). Per configurare in Windows Apache in maniera tale che riconosca Python come linguaggio CGI, sono necessari pochi settaggi di Apache e degli script Python che si creeranno, ben spiegati in questa pagina del team di EditRocket, un code editor.

Dopo avere installato Python, è necessario configurare Apache.
Si devono effettuare un paio di modifiche del file httpd.conf che si trova nella cartella conf del folder di installazione di Apache.
La prima modifica consiste nella modifica della linea:
  Options Indexes FollowSymLinks
aggiungendo ExecCGI , così da trasformarla in:
  Options Indexes FollowSymLinks ExecCGI

La seconda consiste nel decommentare la riga:
  #AddHandler cgi-script .cg
ed aggiungervi Python come linguaggio, modificandola quindi in:
  AddHandler cgi-script .cgi .py

Effettuate queste due modifiche e riavviato il server Apache, gli script Python che creiamo possono essere usati per generare pagine web dinamiche.

Prendiamo il semplice esempio successivo dal testo di Hans Petter Langtangen su Python, Python Scripting for Computational Science.

Creiamo un semplice Hello-World html file ed uno script Python, a nome hw.py, con questo contenuto:

  #!/Python26/python
  import cgi, math

  # required opening of CGI scripts with HTML output:
  print 'Content-type: text/html\n'

  # extract the value of the variable "r" (in the text field):
  form = cgi.FieldStorage()
  r = form.getvalue('r');

  s = str(math.sin(float(r)))
  print 'Hello, World! The sine of %s equals %s' % (r,s)


Notate la prima linea:
  #!/Python26/python

Essa fornisce il percorso all'eseguibile di Python. L'esempio sovrastante si riferisce ad una installazione di Python 2.6 nel folder: c:\Python26.
Se aveste installato Python 2.5 nel folder c:\Programmi\Python25, la prima linea sarebbe:
  #!/Programmi/Python25/python

Il file html Hello World, lanciato dal server locale, apparirà così:

e utilizzando lo script Python genererà una pagina web dinamica che ci illustra il valore del seno del numero inserito nella finestra:

Geolancer?

Un nuovo portale per lavori online, lanciato agli inizi di Aprile e  specifico per "geo-related tasks", a differenza di Elance ed altri che potete eventualmente conoscere. 


La descrizione breve nel loro sito https://www.geolancer.com/ è:
"GeoLancer.com is a complete, intuitive and easy-to-use platform which connects freelancing geo-professionals, the Geo-Providers, with Geo-Buyers who wish to outsource certain Geo-related tasks.
GIS analysis, Remote Sensing imagery processing, Hydrography, Calculations for Land Survey, Geo-referencing, Seismic Data interpretation, Side Scan Sonar mosaicking, Geo-journalism and much more..."


Ovviamente auguriamo loro di riuscire a sfondare.